Class 8 Mathematics Solutions in Assamese
অষ্টম শ্ৰেণীৰ গণিতৰ সমাধান
অনুশীলনী - 3.1
1. নিম্নলিখিত বহুভুজবোৰ আঁকা,
(i) উত্তল ষড়ভুজ

(ii) অৱতল সপ্তভুজ

(iii) অৱতল পঞ্চভুজ

2. নিম্নলিখিত উত্তল বহুভুজবোৰ আঁকা আৰু প্ৰত্যেকৰে কৰ্ণ চিহ্নিত কৰি মুঠ কৰ্ণৰ সংখ্যা লিখা।
(i) সুষম ষড়ভুজ

কৰ্ণৰ সংখ্যা = 9
(ii) অষ্টভুজ

কৰ্ণৰ সংখ্যা = 20
(iii) নৱভুজ
কৰ্ণৰ সংখ্যা = 27
(iv) দশভুজ
কৰ্ণৰ সংখ্যা = 35
3. নিম্নলিখিত সুষম বহুভুজবোৰ আঁকা, প্ৰত্যেকৰে কোণৰ সমষ্টি উলিওৱা আৰু বহুভুজৰ প্ৰতিটো কোণৰ পৰিমাণ কিমান হ'ব উলিওৱা।
(i) সুষম ষড়ভুজ
সমাধানঃ

দিয়া আছে, বাহুৰ সংখ্যা = 6 ডাল
এতেকে, অন্তঃকোণৰ সমষ্টি = (n-2) x 180º
1. নিম্নলিখিত বহুভুজবোৰ আঁকা,
(i) উত্তল ষড়ভুজ

(ii) অৱতল সপ্তভুজ

(iii) অৱতল পঞ্চভুজ

2. নিম্নলিখিত উত্তল বহুভুজবোৰ আঁকা আৰু প্ৰত্যেকৰে কৰ্ণ চিহ্নিত কৰি মুঠ কৰ্ণৰ সংখ্যা লিখা।
(i) সুষম ষড়ভুজ

কৰ্ণৰ সংখ্যা = 9
(ii) অষ্টভুজ

কৰ্ণৰ সংখ্যা = 20
(iii) নৱভুজ
কৰ্ণৰ সংখ্যা = 27
(iv) দশভুজ
কৰ্ণৰ সংখ্যা = 35
3. নিম্নলিখিত সুষম বহুভুজবোৰ আঁকা, প্ৰত্যেকৰে কোণৰ সমষ্টি উলিওৱা আৰু বহুভুজৰ প্ৰতিটো কোণৰ পৰিমাণ কিমান হ'ব উলিওৱা।
(i) সুষম ষড়ভুজ
সমাধানঃ

দিয়া আছে, বাহুৰ সংখ্যা = 6 ডাল
এতেকে, অন্তঃকোণৰ সমষ্টি = (n-2) x 180º
= (6 - 2) x 180º
= 4 x 180º
= 720' এতেকে, প্ৰতিটো অন্তঃকোণ = কোণৰ সমষ্টি/বাহুৰ সংখ্যা
= 720º/6
= 120º
(ii)সুষম নৱভুজ
সমাধানঃ

দিয়া আছে, বাহুৰ সংখ্যা = 9 ডাল
এতেকে, অন্তঃকোণৰ সমষ্টি = (n-2) x 180º
= 1260º/9
= 140º
(iii) 12 সংখ্যক বাহু থকা সুষম বহুভুজ
সমাধানঃ

দিয়া আছে, বাহুৰ সংখ্যা = 12 ডাল
এতেকে, অন্তঃকোণৰ সমষ্টি = (n-2) x 180º
= 1800º/12
= 150º
4. তলৰ চিত্ৰবোৰৰ a, b কোণৰ জোখ উলিওৱা
5. এটা সুষম বহুভুজৰ এটা বহিঃকোণৰ জোখ 30º হ'লে বহুভুজৰ বাহুসংখ্যা কিমান?
সমাধানঃ দিয়া আছে, বহিঃকোণ = 30º
এতেকে, বাহুৰ সংখ্যা = 360º/30º = 12 ডাল
6. 20 টা বাহু বিশিষ্ট এটা সুষম বহুভুজৰ বাহুসংখ্যা কিমান?
সমাধানঃ দিয়া আছে, বাহুৰ সংখ্যা = 20 ডাল
এতেকে, বহিঃকোণ = 360º/20 = 18º
7. তলত একোটা সুষম বহুভুজৰ অন্তঃকোণৰ জোখ দিয়া আছে । বহুভুজকেইটাৰ বাহুৰ সংখ্যা উলিওৱা।
(i) 120º
সমাধানঃ দিয়া আছে, অন্তঃকোণ =120º
এতেকে, বহিঃকোণ = 180º - 120º = 60º
এতেকে, বাহুৰ সংখ্যা = 360º/60º = 6 ডাল
= 720º/6
= 120º
(ii)সুষম নৱভুজ
সমাধানঃ

দিয়া আছে, বাহুৰ সংখ্যা = 9 ডাল
এতেকে, অন্তঃকোণৰ সমষ্টি = (n-2) x 180º
= (9 - 2) x 180º
= 7 x 180º
= 1260º এতেকে, প্ৰতিটো অন্তঃকোণ = কোণৰ সমষ্টি/বাহুৰ সংখ্যা= 1260º/9
= 140º
(iii) 12 সংখ্যক বাহু থকা সুষম বহুভুজ
সমাধানঃ

দিয়া আছে, বাহুৰ সংখ্যা = 12 ডাল
এতেকে, অন্তঃকোণৰ সমষ্টি = (n-2) x 180º
= (12 - 2) x 180º
= 10 x 180º
= 1800º এতেকে, প্ৰতিটো অন্তঃকোণ = কোণৰ সমষ্টি/বাহুৰ সংখ্যা= 1800º/12
= 150º
4. তলৰ চিত্ৰবোৰৰ a, b কোণৰ জোখ উলিওৱা
5. এটা সুষম বহুভুজৰ এটা বহিঃকোণৰ জোখ 30º হ'লে বহুভুজৰ বাহুসংখ্যা কিমান?
সমাধানঃ দিয়া আছে, বহিঃকোণ = 30º
এতেকে, বাহুৰ সংখ্যা = 360º/30º = 12 ডাল
6. 20 টা বাহু বিশিষ্ট এটা সুষম বহুভুজৰ বাহুসংখ্যা কিমান?
সমাধানঃ দিয়া আছে, বাহুৰ সংখ্যা = 20 ডাল
এতেকে, বহিঃকোণ = 360º/20 = 18º
7. তলত একোটা সুষম বহুভুজৰ অন্তঃকোণৰ জোখ দিয়া আছে । বহুভুজকেইটাৰ বাহুৰ সংখ্যা উলিওৱা।
(i) 120º
সমাধানঃ দিয়া আছে, অন্তঃকোণ =120º
এতেকে, বহিঃকোণ = 180º - 120º = 60º
এতেকে, বাহুৰ সংখ্যা = 360º/60º = 6 ডাল
(ii) 144º
সমাধানঃ দিয়া আছে, অন্তঃকোণ =144º
এতেকে, বহিঃকোণ = 180º - 144º = 36º
এতেকে, বাহুৰ সংখ্যা = 360º/36º = 10 ডাল
(iii) 156º
সমাধানঃ দিয়া আছে, অন্তঃকোণ =156º
এতেকে, বহিঃকোণ = 180º - 156º = 24º
এতেকে, বাহুৰ সংখ্যা = 360º/24º = 15 ডাল
এতেকে, বহিঃকোণ = 180º - 156º = 24º
এতেকে, বাহুৰ সংখ্যা = 360º/24º = 15 ডাল
(iv) 135º
সমাধানঃ দিয়া আছে, অন্তঃকোণ =135º
এতেকে, বহিঃকোণ = 180º - 135º = 45º
এতেকে, বাহুৰ সংখ্যা = 360º/45º = 8 ডাল
সমাধানঃ দিয়া আছে, অন্তঃকোণ =135º
এতেকে, বহিঃকোণ = 180º - 135º = 45º
এতেকে, বাহুৰ সংখ্যা = 360º/45º = 8 ডাল
(v) 165º
সমাধানঃ দিয়া আছে, অন্তঃকোণ =165º
এতেকে, বহিঃকোণ = 180º - 165º = 15º
এতেকে, বাহুৰ সংখ্যা = 360º/15º = 24 ডাল
সমাধানঃ দিয়া আছে, অন্তঃকোণ =165º
এতেকে, বহিঃকোণ = 180º - 165º = 15º
এতেকে, বাহুৰ সংখ্যা = 360º/15º = 24 ডাল
8. তলত দিয়া সংখ্যাবোৰ বহুভুজৰ বাহুৰ সংখ্যা হ'লে প্ৰতিটো বহুভুজৰ অন্তঃকোণৰ সমষ্টি উলিওৱা।
(i) 12
সমাধানঃ আমি জানো যে অন্তঃকোণৰ সমষ্টি = (n-2) x 180º, য'ত n = বাহুৰ সংখ্যা
এতেকে, যদি n = 12
তেন্তে, অন্তঃকোণৰ সমষ্টি = (12-2) x 180º
= 10 x 180º
= 1800º
(ii) 14
সমাধানঃ আমি জানো যে অন্তঃকোণৰ সমষ্টি = (n-2) x 180º, য'ত n = বাহুৰ সংখ্যা
এতেকে, যদি n = 14
তেন্তে, অন্তঃকোণৰ সমষ্টি = (14-2) x 180º
= 12 x 180º
= 2160º
(iii) 20
সমাধানঃ আমি জানো যে অন্তঃকোণৰ সমষ্টি = (n-2) x 180º, য'ত n = বাহুৰ সংখ্যা
এতেকে, যদি n = 20
তেন্তে, অন্তঃকোণৰ সমষ্টি = (20-2) x 180º
= 18 x 180º
= 3240º
সমাধানঃ আমি জানো যে অন্তঃকোণৰ সমষ্টি = (n-2) x 180º, য'ত n = বাহুৰ সংখ্যা
এতেকে, যদি n = 20
তেন্তে, অন্তঃকোণৰ সমষ্টি = (20-2) x 180º
= 18 x 180º
= 3240º
(iv) 24
সমাধানঃ আমি জানো যে অন্তঃকোণৰ সমষ্টি = (n-2) x 180º, য'ত n = বাহুৰ সংখ্যা
এতেকে, যদি n = 24
তেন্তে, অন্তঃকোণৰ সমষ্টি = (24-2) x 180º
= 22 x 180º
= 2520º
(v) 25
সমাধানঃ আমি জানো যে অন্তঃকোণৰ সমষ্টি = (n-2) x 180º, য'ত n = বাহুৰ সংখ্যা
এতেকে, যদি n = 25
তেন্তে, অন্তঃকোণৰ সমষ্টি = (25-2) x 180º
= 23 x 180º
= 4140º
9. তলৰ উক্তিবোৰ সঁচা নে মিছা, যুক্তিসহকাৰে লিখা
(i) এটা সুষম বহুভুজৰ প্ৰতিটো বহিঃকোণৰ জোখ 25º হ'ব নোৱাৰে।
সমাধানঃ দিয়া আছে, বহিঃকোণ = 25º
এতেকে, বাহুৰ সংখ্যা = 360º/25º = 14.4 ডাল (যিটো ধনাত্মত অখণ্ড সংখ্যা নহয়)
অৰ্থাৎ, বহিঃকোণৰ জোখ 25º হ'ব নোৱাৰে
এতেকে, সত্য
(ii) এটা সুষম বহুভুজৰ প্ৰতিটো অন্তঃকোণৰ জোখ 1º হ'ব পাৰে।
সমাধানঃ দিয়া আছে, অন্তঃকোণ =1º
এতেকে, বহিঃকোণ = 180º - 1º = 179º
এতেকে, বাহুৰ সংখ্যা = 360º/179º = 2.01 ডাল (যিটো ধনাত্মত অখণ্ড সংখ্যা নহয়)
(iii) এটা সুষম বহুভুজৰ আটাইতকৈ ডাঙৰ বহিঃকোণ 90º
সমাধানঃ দিয়া আছে, বহিঃকোণ = 90º
এতেকে, বাহুৰ সংখ্যা = 360º/90º = 4 ডাল
(iv) এটা সুষম বহুভুজৰ আটাইতকৈ ডাঙৰ অন্তঃকোণ 180º
(v) এটা সুষম বহুভুজৰ আটাইতকৈ সৰু অন্তঃকোণ 60º
2. এটা সামন্তৰিকৰ দুটা সন্নিহিত কোণৰ অনুপাত 4:9 হ'লে সামন্তৰিকৰ কোণৰ জোখ উলিওৱা।
সমাধানঃ ধৰা হ'ল সামন্তৰিকৰ কোণদুটা ক্ৰমে 4x আৰু 9x
আমি জানো যে সামন্তিৰকৰ সন্নিহিত কোণদুটা সম্পূৰক
এতেকে, 4x + 5x = 180º
⇒ 9x = 180º
⇒ x = 180º/9
⇒ x = 20º
এতেকে এটা কোণ = 4 x 20 = 80º
আনটো কোণ = 5 x 20 = 100º
3. এটা সামন্তৰিকৰ দুটা সন্নিহিত কোণৰ এটা আনটোতকৈ 30º বেছি হ'লে সামন্তৰিকৰ প্ৰতিটো কোণৰ জোখ উলিওৱা।
সমাধানঃ ধৰা হ'ল সামন্তৰিকৰ এটা কোণ = x
আনটো কোণ = x + 30º
আমি জানো যে সামন্তিৰকৰ সন্নিহিত কোণদুটা সম্পূৰক
এতেকে, x + (x + 30º) = 180º
⇒ 2x + 30º = 180º
⇒ 2x = 180º - 30º
⇒ 2x = 150º
⇒ x = 150º/2
⇒ x = 75º
সামন্তৰিকৰ এটা কোণ =75º
আনটো কোণ = 75º + 30º = 105º
4. ABCD এটা সামন্তৰিকৰ AC আৰু BD কৰ্ণ, a = 37º আৰু <ABC = 120º হ'লে, b ৰ জোখ কিমান?
সমাধানঃ চিত্ৰৰ বাবে কিতাপৰ সহায় লোৱা (পৃষ্ঠা 67)
আমি জানো যে সামন্তৰিকৰ বিপৰীত কোণবোৰ সমান।
এতেকে, সামন্তৰিক ABCD ৰ ∠D = ∠B
⇒ a + b = 120º
⇒ 37º + b = 120º
⇒ b = 120º - 37º
⇒ b = 83º
5. ABCD আয়তত AC কৰ্ণৰ দৈৰ্ঘ্য 6x - 2 আৰু BD কৰ্ণৰ দৈৰ্ঘ্য 4x + 2 হ'লে, x ৰ মান আৰু AC ৰ দৈৰ্ঘ্য উলিওৱা।
সমাধানঃ
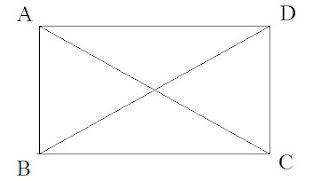
দিয়া আছে, ABCD আয়তৰ কৰ্ণ AC = 6x - 2
কৰ্ণ BD = 4x + 2
আমি জানো যে আয়তৰ কৰ্ণদুডাল সমান দৈৰ্ঘ্যৰ
এতেকে, AC = BD
⇒ 6x - 2 = 4x + 2
⇒ 6x - 4x = 2 + 2
⇒ 2x = 4
⇒ x = 4/2
⇒ x = 2
এতেকে, AC = 6 x 2 - 2 = 12 - 2 = 10
6. ABCD আয়তৰ দুডাল কৰ্ণই O বিন্দুত মিলিত হয় । AC আৰু BD ৰ দৈৰ্ঘ্য 3x + 1 আৰু 8x - 24 হ'লে, x, AO আৰু BO মান উলিওৱা।
সমাধানঃ

আমি জানো যে আয়তৰ কৰ্ণদুডাল পৰস্পৰ সমান
এতেকে, AC = BD
⇒ 3x + 1 = 8x - 24
⇒ 3x - 8x = -24 - 1
⇒ -5x = -25
⇒ 5x = 25
⇒ x = 25/5
⇒ x = 5
এতেকে AC = 3 x 5 + 1 = 15 + 1 = 16
আনহাতে আয়তৰ কৰ্ণবোৰ পৰস্পৰ সমদ্বিখণ্ডত হয়
AO = BO = 16/2 = 8 একক
7. ABCD বৰ্গত ∠A = 4x + 30º হ'লে, x ৰ মান উলিওৱা।
সমাধানঃ আমি জানো যে বৰ্গৰ প্ৰতিটো কোণ = 90º
এতেকে, ABCD বৰ্গত ∠A = 90'
⇒ 4x + 30º = 90º
⇒ 4x = 90º - 30º
⇒ x = 60º/4
⇒ x = 15º
8. ABCD আয়তৰ AB = 2x + 5, BC = 20 আৰু AD = 3x + 5 হ'লে আয়তৰ চাৰিটা বাহুৰ যোগফল নিৰ্ণয় কৰা।
সমাধানঃ ABCD আয়তৰ,
AB = 2x + 5
BC = 20
AD = 3x + 5
যিহেতু, আয়তৰ বিপৰীত বাহু সমান,
এতেকে, AD = BC
⇒ 3x + 5 = 20
⇒ 3x = 20 - 5
⇒ 3x = 15
⇒ x = 15/5
⇒ x = 5
এতেকে, AB = 2 x 5 + 5 = 10 + 5 = 15
এতেকে, চাৰিটা বাহুৰ যোগফল = পৰিসীমা = 2 x (দীঘ + প্ৰস্থ)
= 2(20 + 15)
= 2 x 35
= 70 cm
Answer: 70 cm
9. ABCD সামন্তৰিক এটাত ∠B = 2x + 10º আৰু ∠D = 3x - 13º হ'লে সামন্তৰিকৰ আটাইকেইটা কোণৰ পৰিমাণ উলিওৱা।
সমাধানঃ আমি জানো যে সামন্তৰিকৰ বিপৰীত কোণবোৰ সমান।
এতেকে, ∠B = ∠D
⇒ (2x + 10º) = (3x - 13º)
⇒ 2x - 3x = -13º - 10º
⇒ -x = -23º
⇒ x = 23º
এতেকে, ∠B = ∠D = 2x + 10º = 2 x 23 + 10 = 56º
আনহাতে, সামন্তৰিকৰ সন্নিহিত কোণবোৰ সম্পূৰক।
এতেকে, <A + <B = 180º
⇒ <A = 180º - <B
⇒ <A = 180º - 56º
⇒ <A = 124º
Answer: 124º, 56º, 124º, 56º
10. এটা বৰ্গৰ চাৰিটা বাহুৰ যোগফল 36 চেমি হ'লে বৰ্গৰ বাহুৰ দীঘ উলিওৱা।
সমাধানঃ ধৰা হ'ল বৰ্গৰ প্ৰতিটো বাহু = x
আমি জানো যে বৰ্গৰ চাৰিটা বাহু সমান
এতেকে, a + a + a + a = 36 cm
⇒ 4a = 36
⇒ 4a = 36
⇒ a = 36/4
⇒ a = 9 cm
11. ABCD ৰম্বাছত AB = 3x + 4 আৰু BC = 2x + 7 হ'লে DC আৰু AD বাহুৰ দীঘ কিমান?
সমাধানঃ দিয়া আছে ABCD ৰম্বাছত AB = 3x + 4 আৰু BC = 2x + 7
∴ AB = BC = DC = AD = 2x + 7 = 2×3+7= 6+7= 13cm
সমাধানঃ দিয়া আছে, অন্তঃকোণ =1º
এতেকে, বহিঃকোণ = 180º - 1º = 179º
এতেকে, বাহুৰ সংখ্যা = 360º/179º = 2.01 ডাল (যিটো ধনাত্মত অখণ্ড সংখ্যা নহয়)
অৰ্থাৎ, অন্তঃকোণৰ জোখ 1º হ'ব নোৱাৰে
এতেকে, অসত্য
সমাধানঃ দিয়া আছে, বহিঃকোণ = 90º
এতেকে, বাহুৰ সংখ্যা = 360º/90º = 4 ডাল
কিন্তু বহুভুজ গঠনৰ বাবে নুন্যতম তিনিডাল বাহু হ'লেও হয়
অৰ্থাৎ, বহিঃকোণৰ সৰ্বোচ্চ জোখ 90º হ'ব নোৱাৰে
এতেকে, অসত্য
(iv) এটা সুষম বহুভুজৰ আটাইতকৈ ডাঙৰ অন্তঃকোণ 180º
সমাধানঃ দিয়া আছে, অন্তঃকোণ =180º
এতেকে, বহিঃকোণ = 180º - 180º = 0º
এতেকে, বাহুৰ সংখ্যা = 360º/0º = সংজ্ঞাবদ্ধ নহয়
এতেকে, বহিঃকোণ = 180º - 180º = 0º
এতেকে, বাহুৰ সংখ্যা = 360º/0º = সংজ্ঞাবদ্ধ নহয়
অৰ্থাৎ, অন্তঃকোণৰ সৰ্বোচ্চ জোখ 180º হ'ব নোৱাৰে
এতেকে, অসত্য
সমাধানঃ দিয়া আছে, অন্তঃকোণ =60º
এতেকে, বহিঃকোণ = 180º - 60º = 120º
এতেকে, বাহুৰ সংখ্যা = 360º/120º = 3
এতেকে, বহিঃকোণ = 180º - 60º = 120º
এতেকে, বাহুৰ সংখ্যা = 360º/120º = 3
কিন্তু বহুভুজ গঠনৰ বাবে নুন্যতম তিনিডাল বাহু হ'লেও হয়
অৰ্থাৎ, অন্তঃকোণৰ সৰ্বনিম্ন জোখ 60º হ'ব পাৰে।
এতেকে, সত্যঅনুশীলনী - 3.2
1. তলত দিয়া বিভিন্ন চতুৰ্ভুজত থকা অজ্ঞাত ৰাশি (বাহু/কোণ) ৰ মান উলিওৱা । ইয়াত চতুৰ্ভুজবোৰৰ বিপৰীত বাহুত থকা কাঁড় চিনে (>) বাহুযোৰ সমান্তৰাল হোৱা বুজাইছে ।
(i) চিত্ৰৰ বাবে কিতাপৰ সহায় লোৱা (পৃষ্ঠা 66)
সমাধানঃ ধৰা হ'ল ABCD চতুৰ্ভুজৰ
∠A = 110º
∠B = a
∠C = 75º
∠D = 80º
আমি জানো যে চতুৰ্ভুজৰ চাৰিটা কোণৰ সমষ্টি = 360º
⇒ ∠A + ∠B + ∠C + ∠D = 360º
⇒ 110º + a + 75º + 80º = 360º
⇒ a + 265º = 360º
⇒ a = 360º - 265º
⇒ a = 95º
(ii) চিত্ৰৰ বাবে কিতাপৰ সহায় লোৱা (পৃষ্ঠা 66)
সমাধানঃ ধৰা হল ABCD চতুৰ্ভুজৰ
∠A = a
∠B = b
∠C = c
∠D = 105º
দিয়া আছে, BC||AD, CD ছেদক
এতেকে, ∠C + ∠D = 180º (ছেদকৰ একেফালৰ অন্তঃকোণ)
⇒ c + 105º = 180º
⇒ c = 180º - 105º
⇒ c = 75º
একেদৰেই, AB||CD, AD ছেদক
এতেকে, ∠A + 105º = 180º (ছেদকৰ একেফালৰ অন্তঃকোণ)
⇒ a + 105º = 180º
⇒ a = 180º - 105º
⇒ a = 75º
একেদৰেই, BC||AD, AB ছেদক
এতেকে, ∠A + ∠B = 180º (ছেদকৰ একেফালৰ অন্তঃকোণ)
⇒ a + b = 180º
⇒ 75º + b = 180º
⇒ b = 180º - 75º
⇒ b = 105º
Answer: a = 75º, b = 105º, c = 75º
(ii) চিত্ৰৰ বাবে কিতাপৰ সহায় লোৱা (পৃষ্ঠা 66)
সমাধানঃ ধৰা হল ABCD চতুৰ্ভুজৰ
∠A = 110º
∠D = 40º + b
দিয়া আছে, AB||CD, AD ছেদক
এতেকে, ∠A + ∠D = 180º (ছেদকৰ একেফালৰ অন্তঃকোণ)
⇒ 110º + (40º + b) = 180º
⇒ 150º + b = 180º
⇒ b = 180º - 150º
⇒ b = 30º
আকৌ, BC||AD, BD ছেদক
এতেকে, a = b = 30º (একান্তৰ কোণ)
(iv) চিত্ৰৰ বাবে কিতাপৰ সহায় লোৱা (পৃষ্ঠা 66)
সমাধানঃ ধৰা হ'ল ABCD চতুৰ্ভুজৰ
AB =2b + 1
BC = 24
CD = 9
AD = 4a
যিহেতু চতুৰ্ভুজৰ বিপৰীত বাহুবোৰ সমান আৰু সমান্তৰাল
এতেকে, AB = CD
⇒ 2b + 1 = 9
⇒ 2b = 9 - 1
⇒ b = 8/2
⇒ b = 4
একেদৰেই, AD = BC
⇒ 4a = 24
⇒ a = 24/4
⇒ a = 6
2. এটা সামন্তৰিকৰ দুটা সন্নিহিত কোণৰ অনুপাত 4:9 হ'লে সামন্তৰিকৰ কোণৰ জোখ উলিওৱা।
সমাধানঃ ধৰা হ'ল সামন্তৰিকৰ কোণদুটা ক্ৰমে 4x আৰু 9x
আমি জানো যে সামন্তিৰকৰ সন্নিহিত কোণদুটা সম্পূৰক
এতেকে, 4x + 5x = 180º
⇒ 9x = 180º
⇒ x = 180º/9
⇒ x = 20º
এতেকে এটা কোণ = 4 x 20 = 80º
আনটো কোণ = 5 x 20 = 100º
3. এটা সামন্তৰিকৰ দুটা সন্নিহিত কোণৰ এটা আনটোতকৈ 30º বেছি হ'লে সামন্তৰিকৰ প্ৰতিটো কোণৰ জোখ উলিওৱা।
সমাধানঃ ধৰা হ'ল সামন্তৰিকৰ এটা কোণ = x
আনটো কোণ = x + 30º
আমি জানো যে সামন্তিৰকৰ সন্নিহিত কোণদুটা সম্পূৰক
এতেকে, x + (x + 30º) = 180º
⇒ 2x + 30º = 180º
⇒ 2x = 180º - 30º
⇒ 2x = 150º
⇒ x = 150º/2
⇒ x = 75º
সামন্তৰিকৰ এটা কোণ =75º
আনটো কোণ = 75º + 30º = 105º
4. ABCD এটা সামন্তৰিকৰ AC আৰু BD কৰ্ণ, a = 37º আৰু <ABC = 120º হ'লে, b ৰ জোখ কিমান?
সমাধানঃ চিত্ৰৰ বাবে কিতাপৰ সহায় লোৱা (পৃষ্ঠা 67)
আমি জানো যে সামন্তৰিকৰ বিপৰীত কোণবোৰ সমান।
এতেকে, সামন্তৰিক ABCD ৰ ∠D = ∠B
⇒ a + b = 120º
⇒ 37º + b = 120º
⇒ b = 120º - 37º
⇒ b = 83º
5. ABCD আয়তত AC কৰ্ণৰ দৈৰ্ঘ্য 6x - 2 আৰু BD কৰ্ণৰ দৈৰ্ঘ্য 4x + 2 হ'লে, x ৰ মান আৰু AC ৰ দৈৰ্ঘ্য উলিওৱা।
সমাধানঃ

দিয়া আছে, ABCD আয়তৰ কৰ্ণ AC = 6x - 2
কৰ্ণ BD = 4x + 2
আমি জানো যে আয়তৰ কৰ্ণদুডাল সমান দৈৰ্ঘ্যৰ
এতেকে, AC = BD
⇒ 6x - 2 = 4x + 2
⇒ 6x - 4x = 2 + 2
⇒ 2x = 4
⇒ x = 4/2
⇒ x = 2
এতেকে, AC = 6 x 2 - 2 = 12 - 2 = 10
6. ABCD আয়তৰ দুডাল কৰ্ণই O বিন্দুত মিলিত হয় । AC আৰু BD ৰ দৈৰ্ঘ্য 3x + 1 আৰু 8x - 24 হ'লে, x, AO আৰু BO মান উলিওৱা।
সমাধানঃ

আমি জানো যে আয়তৰ কৰ্ণদুডাল পৰস্পৰ সমান
এতেকে, AC = BD
⇒ 3x + 1 = 8x - 24
⇒ 3x - 8x = -24 - 1
⇒ -5x = -25
⇒ 5x = 25
⇒ x = 25/5
⇒ x = 5
এতেকে AC = 3 x 5 + 1 = 15 + 1 = 16
আনহাতে আয়তৰ কৰ্ণবোৰ পৰস্পৰ সমদ্বিখণ্ডত হয়
AO = BO = 16/2 = 8 একক
7. ABCD বৰ্গত ∠A = 4x + 30º হ'লে, x ৰ মান উলিওৱা।
সমাধানঃ আমি জানো যে বৰ্গৰ প্ৰতিটো কোণ = 90º
এতেকে, ABCD বৰ্গত ∠A = 90'
⇒ 4x + 30º = 90º
⇒ 4x = 90º - 30º
⇒ x = 60º/4
⇒ x = 15º
8. ABCD আয়তৰ AB = 2x + 5, BC = 20 আৰু AD = 3x + 5 হ'লে আয়তৰ চাৰিটা বাহুৰ যোগফল নিৰ্ণয় কৰা।
সমাধানঃ ABCD আয়তৰ,
AB = 2x + 5
BC = 20
AD = 3x + 5
যিহেতু, আয়তৰ বিপৰীত বাহু সমান,
এতেকে, AD = BC
⇒ 3x + 5 = 20
⇒ 3x = 20 - 5
⇒ 3x = 15
⇒ x = 15/5
⇒ x = 5
এতেকে, AB = 2 x 5 + 5 = 10 + 5 = 15
এতেকে, চাৰিটা বাহুৰ যোগফল = পৰিসীমা = 2 x (দীঘ + প্ৰস্থ)
= 2(20 + 15)
= 2 x 35
= 70 cm
Answer: 70 cm
9. ABCD সামন্তৰিক এটাত ∠B = 2x + 10º আৰু ∠D = 3x - 13º হ'লে সামন্তৰিকৰ আটাইকেইটা কোণৰ পৰিমাণ উলিওৱা।
সমাধানঃ আমি জানো যে সামন্তৰিকৰ বিপৰীত কোণবোৰ সমান।
এতেকে, ∠B = ∠D
⇒ (2x + 10º) = (3x - 13º)
⇒ 2x - 3x = -13º - 10º
⇒ -x = -23º
⇒ x = 23º
এতেকে, ∠B = ∠D = 2x + 10º = 2 x 23 + 10 = 56º
আনহাতে, সামন্তৰিকৰ সন্নিহিত কোণবোৰ সম্পূৰক।
এতেকে, <A + <B = 180º
⇒ <A = 180º - <B
⇒ <A = 180º - 56º
⇒ <A = 124º
Answer: 124º, 56º, 124º, 56º
10. এটা বৰ্গৰ চাৰিটা বাহুৰ যোগফল 36 চেমি হ'লে বৰ্গৰ বাহুৰ দীঘ উলিওৱা।
সমাধানঃ ধৰা হ'ল বৰ্গৰ প্ৰতিটো বাহু = x
আমি জানো যে বৰ্গৰ চাৰিটা বাহু সমান
এতেকে, a + a + a + a = 36 cm
⇒ 4a = 36
⇒ 4a = 36
⇒ a = 36/4
⇒ a = 9 cm
11. ABCD ৰম্বাছত AB = 3x + 4 আৰু BC = 2x + 7 হ'লে DC আৰু AD বাহুৰ দীঘ কিমান?
সমাধানঃ দিয়া আছে ABCD ৰম্বাছত AB = 3x + 4 আৰু BC = 2x + 7
আমি জানো যে ৰম্বাছৰ চাৰিডাল সন্নিহিত বাহু সমান।
∴ AB = BC
⇒ 3x + 4 = 2x + 7
⇒ 3x − 2x = 7 − 4
⇒ x = 3
∴ AB = BC = DC = AD = 2x + 7 = 2×3+7= 6+7= 13cm
12. ABCD সামন্তৰিকত AC আৰু BD কৰ্ণই E বিন্দুত সমদ্বিখণ্ডিত হয়। যদি AE = 10x তেন্তে AC ৰ জোখ উলিওৱা যদি x = 3 হয়।
সমাধানঃ যিহেতু, ABCD সামন্তৰিকত AC আৰু BD কৰ্ণই E বিন্দুত সমদ্বিখণ্ডিত হয়।
∴ E, AC ৰ মধ্যবিন্দু।
অৰ্থাৎ AC = 2AE
⇒ AC = 2×10x = 20x = 20×3=60cm
16. এটা চতুৰ্ভুজৰ চাৰিটা কোণৰ অনুপাত 3:4:5:6 হ'লে চতুৰ্ভুজৰ কোণবোৰৰ জোখ উলিওৱা।
সমাধানঃ ধৰা হ'ল চতুৰ্ভুজৰ চাৰিটা কোণ ক্ৰমে 3x, 4x, 5x, 6x
এতেকে, 1ম কোণ = 3 x 20 = 60º
2য় কোণ = 4 x 20 = 80º
3য় কোণ = 5 x 20 = 100º
4ৰ্থ কোণ = 6 x 20 = 120º
সমাধানঃ ধৰা হ'ল চতুৰ্ভুজৰ চাৰিটা কোণ ক্ৰমে 3x, 4x, 5x, 6x
আমি জানো যে চতুৰ্ভুজৰ চাৰিটা কোণৰ সমষ্টি = 360º
⇒ 3x + 4x + 5x + 6x = 360º
⇒ 18x = 360º
⇒ x = 360º/18
⇒ x = 20ºএতেকে, 1ম কোণ = 3 x 20 = 60º
2য় কোণ = 4 x 20 = 80º
3য় কোণ = 5 x 20 = 100º
4ৰ্থ কোণ = 6 x 20 = 120º

.png)





Nice
ReplyDeleteNice
DeleteRaj
ReplyDeleteGood
ReplyDeleteGood
ReplyDeleteRydyd
ReplyDeleteMoja
ReplyDelete